Determinants are mathematical objects that are very useful in the analysis and solution of systems of linear equations. As shown by Cramer's rule, a nonhomogeneous system of linear equations has a unique solution iff the determinant of the system's matrix is nonzero (i.e., the matrix is nonsingular). For example, eliminating , , and from the equations

			(1)
			(2)
			(3)

gives the expression

(4)

which is called the determinant for this system of equation. Determinants are defined only for square matrices.

If the determinant of a matrix is 0, the matrix is said to be singular, and if the determinant is 1, the matrix is said to be unimodular.

The determinant of a matrix ,

(5)

is commonly denoted , , or in component notation as , , or (Muir 1960, p. 17). Note that the notation may be more convenient when indicating the absolute value of a determinant, i.e., instead of . The determinant is implemented in Mathematica as Det[m].

A determinant is defined to be

(6)

A determinant can be expanded "by minors" to obtain

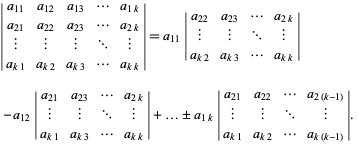(7)

A general determinant for a matrix has a value

(8)

with no implied summation over and where (also denoted ) is the cofactor of defined by

(9)

and is the minor of matrix formed by eliminating row and column from . This process is called determinant expansion by minors (or "Laplacian expansion by minors," sometimes further shortened to simply "Laplacian expansion").

A determinant can also be computed by writing down all permutations of , taking each permutation as the subscripts of the letters , , ..., and summing with signs determined by , where is the number of permutation inversions in permutation (Muir 1960, p. 16), and is the permutation symbol. For example, with , the permutations and the number of inversions they contain are 123 (0), 132 (1), 213 (1), 231 (2), 312 (2), and 321 (3), so the determinant is given by

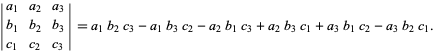(10)

If is a constant and an square matrix, then

(11)

Given an determinant, the additive inverse is

(12)

Determinants are also distributive, so

(13)

This means that the determinant of a matrix inverse can be found as follows:

(14)

where is the identity matrix, so

(15)

Determinants are multilinear in rows and columns, since

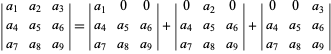(16)

and

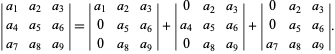(17)

The determinant of the similarity transformation of a matrix is equal to the determinant of the original matrix

			(18)
			(19)
			(20)

The determinant of a similarity transformation minus a multiple of the unit matrix is given by

			(21)
			(22)
			(23)
			(24)

The determinant of a matrix transpose equals the determinant of the original matrix,

(25)

and the determinant of a complex conjugate is equal to the complex conjugate of the determinant

(26)

Let be a small number. Then

(27)

where is the matrix trace of . The determinant takes on a particularly simple form for a triangular matrix

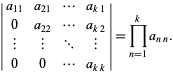(28)

Important properties of the determinant include the following, which include invariance under elementary row and column operations.

1. Switching two rows or columns changes the sign.

2. Scalars can be factored out from rows and columns.

3. Multiples of rows and columns can be added together without changing the determinant's value.

4. Scalar multiplication of a row by a constant multiplies the determinant by .

5. A determinant with a row or column of zeros has value 0.

6. Any determinant with two rows or columns equal has value 0.

Property 1 can be established by induction. For a matrix, the determinant is

			(29)
			(30)
			(31)

For a matrix, the determinant is

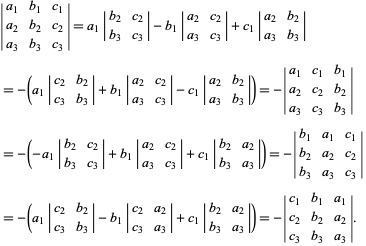(32)

Property 2 follows likewise. For and matrices,

			(33)
			(34)

and

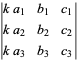			(35)
			(36)

Property 3 follows from the identity

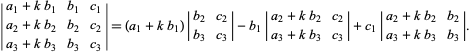(37)

If is an matrix with real numbers, then has the interpretation as the oriented -dimensional content of the parallelepiped spanned by the column vectors , ..., in . Here, "oriented" means that, up to a change of or sign, the number is the -dimensional content, but the sign depends on the "orientation" of the column vectors involved. If they agree with the standard orientation, there is a sign; if not, there is a sign. The parallelepiped spanned by the -dimensional vectors through is the collection of points

(38)

where is a real number in the closed interval .

Several accounts state that Lewis Carroll (Charles Dodgson) sent Queen Victoria a copy of one of his mathematical works, in one account, An Elementary Treatise on Determinants. Heath (1974) states, "A well-known story tells how Queen Victoria, charmed by Alice in Wonderland, expressed a desire to receive the author's next work, and was presented, in due course, with a loyally inscribed copy of An Elementary Treatise on Determinants," while Gattegno (1974) asserts "Queen Victoria, having enjoyed Alice so much, made known her wish to receive the author's other books, and was sent one of Dodgson's mathematical works." However, in Symbolic Logic (1896), Carroll stated, "I take this opportunity of giving what publicity I can to my contradiction of a silly story, which has been going the round of the papers, about my having presented certain books to Her Majesty the Queen. It is so constantly repeated, and is such absolute fiction, that I think it worth while to state, once for all, that it is utterly false in every particular: nothing even resembling it has occurred" (Mikkelson and Mikkelson).

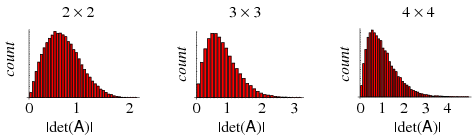
Hadamard (1893) showed that the absolute value of the determinant of a complex matrix with entries in the unit disk satisfies

(39)

(Brenner 1972). The plots above show the distribution of determinants for random complex matrices with entries satisfying for , 3, and 4.