Advertisement
UTeM BMFR Google Search Engine
Custom Search
Bernoulli Theorem Design Equations and Formulas Calculator
Fluid Mechanics and Hydraulics
Solving For Head Loss
Inputs:
Conversions:
| Z1 | = | 0 | = | 0 | foot | |
| Z2 | = | 0 | = | 0 | foot | |
| P1 | = | 0 | = | 0 | pound/foot^2 | |
| P2 | = | 0 | = | 0 | pound/foot^2 | |
| V1 | = | 0 | = | 0 | foot/second | |
| V2 | = | 0 | = | 0 | foot/second | |
| p | = | 0 | = | 0 | pound/foot^3 | |
| g | = | 0 | = | 0 | foot/second^2 |
Solution:
| head loss (h) | = | HAS NOT BEEN CALCULATED | |
Other Units:
Change Equation
Note Bernoulli Equation Assumes:
Select an equation to solve for a different unknown
Where
Note Bernoulli Equation Assumes:
| 1. | flow is streamline |
| 2. | steady state flow |
| 3. | inviscid fluid |
| 4. | incompressible fluid |
Select an equation to solve for a different unknown
 | Solve for head loss |
 | Solve for static head or elevation at point 1 |
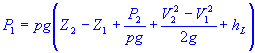 | Solve for pressure at point 1 |
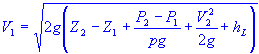 | Solve for velocity at point 1 |
Where
| h | = | head loss |
| Z | = | static head or elevation |
| P | = | Pressure |
| V | = | fluid velocity |
| p | = | fluid density |
| g | = | acceleration of gravity |
| Q | = | flow rate |
Reference - Books:
1) P. Aarne Vesilind, J. Jeffrey Peirce and Ruth F. Weiner. 1994. Environmental Engineering. Butterworth Heinemann. 3rd ed.
0 Comments:
Subscribe to:
Post Comments (Atom)
