UTeM BMFR Google Search Engine

A procedure for decomposing an ![]() matrix
matrix ![]() into a product of a lower triangular matrix
into a product of a lower triangular matrix ![]() and an upper triangular matrix
and an upper triangular matrix ![]() ,
,
| (1) |
LU decomposition is implemented in Mathematica as LUDecomposition[m].
Written explicitly for a ![]() matrix, the decomposition is
matrix, the decomposition is
![[l_(11) 0 0; l_(21) l_(22) 0; l_(31) l_(32) l_(33)][u_(11) u_(12) u_(13); 0 u_(22) u_(23); 0 0 u_(33)]=[a_(11) a_(12) a_(13); a_(21) a_(22) a_(23); a_(31) a_(32) a_(33)]](http://mathworld.wolfram.com/images/equations/LUDecomposition/NumberedEquation2.gif) | (2) |
![[l_(11)u_(11) l_(11)u_(12) l_(11)u_(13); l_(21)u_(11) l_(21)u_(12)+l_(22)u_(22) l_(21)u_(13)+l_(22)u_(23); l_(31)u_(11) l_(31)u_(12)+l_(32)u_(22) l_(31)u_(13)+l_(32)u_(23)+l_(33)u_(33)]=[a_(11) a_(12) a_(13); a_(21) a_(22) a_(23); a_(31) a_(32) a_(33)].](http://mathworld.wolfram.com/images/equations/LUDecomposition/NumberedEquation3.gif) | (3) |
This gives three types of equations
| (4) | |
| (5) | |
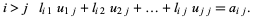 j l_(i1)u_(1j)+l_(i2)u_(2j)+...+l_(ij)u_(jj)=a_(ij). " width="240" border="0" height="18"> j l_(i1)u_(1j)+l_(i2)u_(2j)+...+l_(ij)u_(jj)=a_(ij). " width="240" border="0" height="18"> | (6) |
This gives ![]() equations for
equations for ![]() unknowns (the decomposition is not unique), and can be solved using Crout's method. To solve the matrix equation
unknowns (the decomposition is not unique), and can be solved using Crout's method. To solve the matrix equation
| (7) |
first solve ![]() for
for ![]() . This can be done by forward substitution
. This can be done by forward substitution
| (8) | |||
| (9) |
for ![]() , ...,
, ..., ![]() . Then solve
. Then solve ![]() for
for ![]() . This can be done by back substitution
. This can be done by back substitution
| (10) | |||
| (11) |
for ![]() , ..., 1.
, ..., 1.
Related Keyword:Gaussian Elimination, Lower Triangular Matrix, Matrix Decomposition, Cholesky Decomposition, QR Decomposition, Triangular Matrix, Upper Triangular Matrix
Labels: Numerical Method













