Nonhomogeneous matrix equations of the form

(1)

can be solved by taking the matrix inverse to obtain

(2)

This equation will have a nontrivial solution iff the determinant . In general, more numerically stable techniques of solving the equation include Gaussian elimination, LU decomposition, or the square root method.

For a homogeneous matrix equation

(3)

to be solved for the s, consider the determinant

(4)

Now multiply by , which is equivalent to multiplying the first column (or any column) by ,

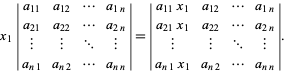(5)

The value of the determinant is unchanged if multiples of columns are added to other columns. So add times column 2, ..., and times column to the first column to obtain

(6)

But from the original matrix, each of the entries in the first columns is zero since

(7)

so

(8)

Therefore, if there is an which is a solution, the determinant is zero. This is also true for , ..., , so the original homogeneous system has a nontrivial solution for all s only if the determinant is 0. This approach is the basis for Cramer's rule.

Given a numerical solution to a matrix equation, the solution can be iteratively improved using the following technique. Assume that the numerically obtained solution to

(9)

is , where is an error term. The first solution therefore gives

(10)

(11)

where is found by solving (10)

(12)

Combining (11) and (12) then gives

(13)